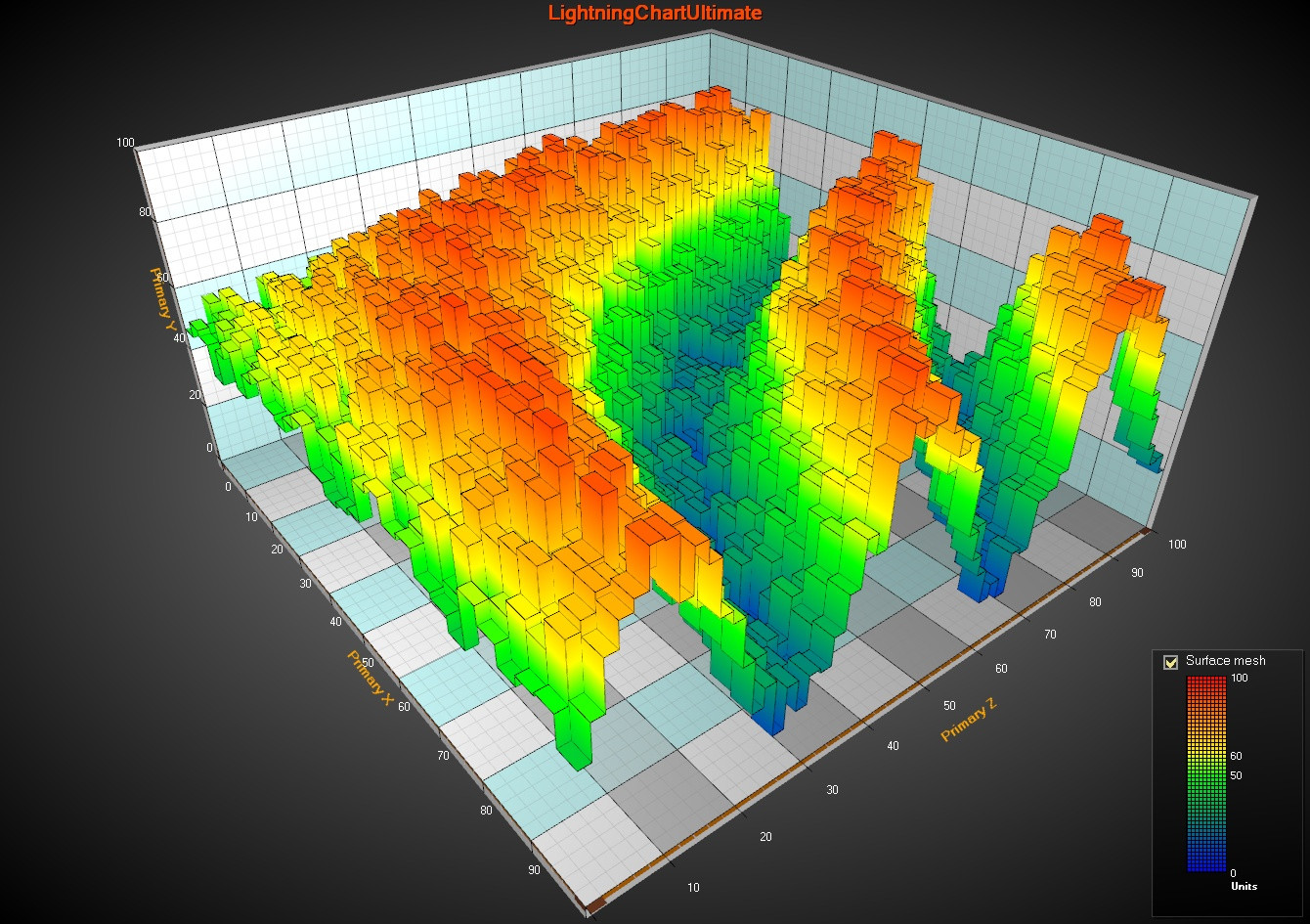
Why Plotting Matters

If your data looks good, people trust it more. Graphs and Charts are easier for anybody to understand than a .csv file or database entries as they require much less technical knowledge to understand.

Examples of financial plots (MPL)

Time Series Plot

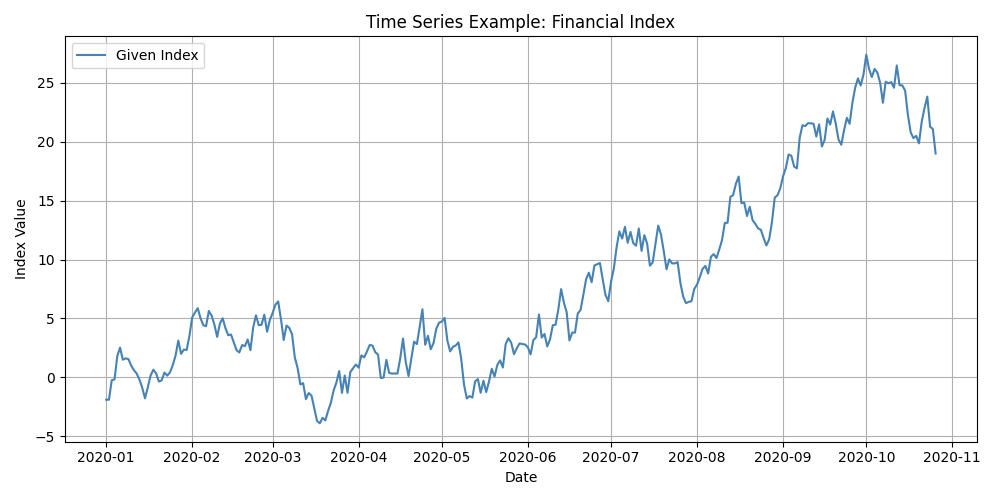
Time Series Plot

Description:
A time series plot visualises data points indexed in time order. It’s commonly used to observe trends, seasonal patterns, or anomalies over a continuous period.

Purpose:
To analyse how a variable changes over time.

Use Cases:

  • Financial markets (e.g., stock prices, index performance)

  • Economic indicators (e.g., inflation, unemployment)

  • Scientific measurements over time (e.g., temperature, growth rates)

Insight Provided:
Highlights trends, cycles, and potential outliers or regime shifts in the data.

Histogram

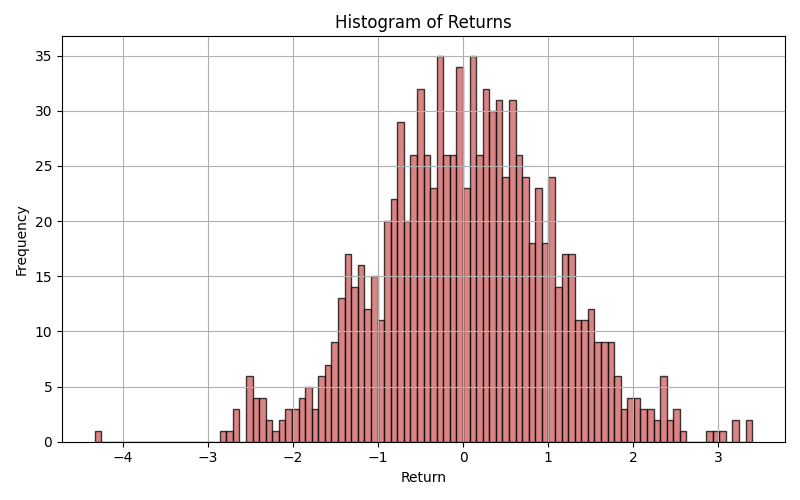
Time Series Plot

Description:
A histogram shows the distribution of a single continuous variable by dividing it into intervals (bins) and counting how many data points fall into each.

Purpose:
To understand the shape, central tendency, and spread of a distribution.

Use Cases:

  • Analysing returns or error distributions

  • Assessing normality in statistical testing

  • Identifying skewness or outliers

Insight Provided:
Reveals whether data is normally distributed, skewed, or has heavy tails—crucial for selecting proper statistical models.

Box Plot (Box-and-Whisker Plot)

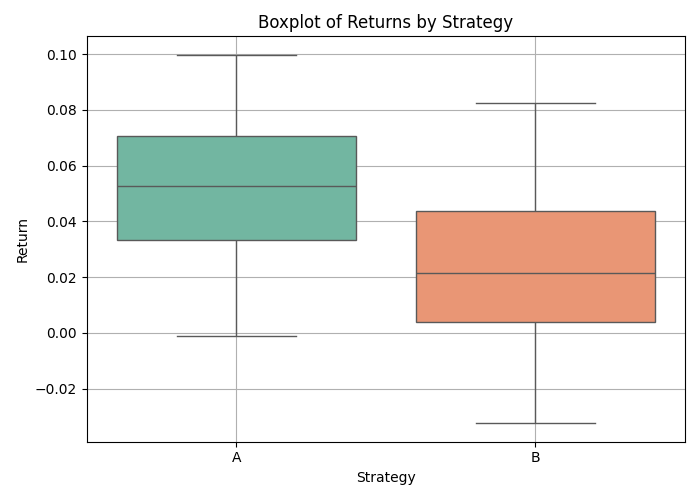
Time Series Plot

Description:
Box plots display the distribution of a variable through its quartiles and highlight potential outliers.

Purpose:
To compare distributions across categories or groups, especially in terms of spread and central location.

Use Cases:

  • Comparing performance of algorithms or strategies

  • Visualising risk/return trade-offs

  • Identifying outliers in clinical or financial data

Insight Provided:
Summarises five-number statistics: minimum, Q1, median, Q3, and maximum. Helps detect asymmetry and variability between groups.

Scatter Plot with Regression Line

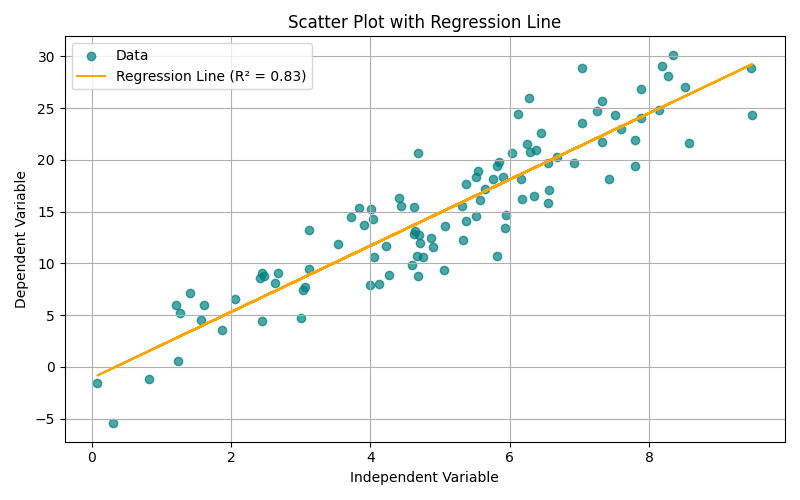
Time Series Plot

Description:
A scatter plot visualises the relationship between two continuous variables. Adding a regression line indicates the direction and strength of linear association.

Purpose:
To assess correlation, causality assumptions, and model fitness.

Use Cases:

  • Regression analysis in econometrics or machine learning

  • Portfolio risk vs. return assessment

  • Marketing: advertising spend vs. revenue

Insight Provided:
Visual representation of correlation (positive, negative, or none), and strength of linear trend. Regression line gives predictive value.